|
|
|
بِسْــــــــــــــــــــــمِ اﷲِارَّحْمَنِ ارَّحِيم
 _____________________________
*****************************
Bundan 20 yıl sonra, yaptıkların değil, yapmadıkların için üzüleceksin…Dolayısıyla halatları çöz.Limandan uzaklara yelken aç. Rüzgârı yakala, araştır, düşle, keşfet. Yapabileceğin kadar söz ver. Sonra söz verdiğinden daha fazlasını yap. Oturarak Başarıya ulaşan tek yaratık tavuktur. Dalın ucuna gitmekten korkma. Meyve oradadır. Günün sonunda Kendini bir sokak köpeği gibi yorgun duyumsuyorsan, bu belki tüm gün hırladığın içindir. HAYATTA YA TOZU DUMANA KATARSIN YA DA TOZU DUMANI YUTARSIN. İyi çalışan, sık gülen ve çok seven başarıyı elde eder. İnsanın tüm evrende kesin olarak düzeltebileceğin tek şey vardır : Kendisi…
Aldous HUXLEY
_____________________________
*****************************
__________________________
___________________
|
|
 |
Bir cismin ağırlığının uygulama noktasına o cismin ağırlık merkezi denir. Ağırlık merkezi G harfi ile gösterilir. Bazı geometrik şekilli türdeş cisimlerin ağırlık merkezleri aşağıda gösterilmiştir.
 
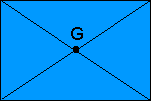
Şekildeki karenin ve dikdörtgenin ağırlık merkezi köşegenlerinin kesim noktasıdır.
çember daire küre
  
Çember, daire ve kürenin ağırlık merkezleri şekillerin geometrik merkezidir.
Türdeş çubuğun ağırlık merkezi tam ortasıdır.
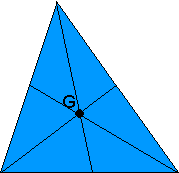
Üçgenin ağırlık merkezi kenarortayların kesiştiği noktadır. Kenarortayların kesim noktası kenarortayı köşeden 2, kenardan 1 birim uzunluğunda keser.
Dikdörtgenler prizması veya küp şeklindeki cisimlerin ağırlık merkezi tam ortalarıdır. Bu nokta aynı zamanda cisim köşegenlerinin kesim noktasıdır.
 
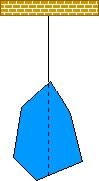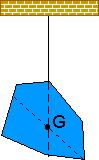
şekil 1 şekil 2
Düzgün şekilli olmayan cisimlerin ağırlık merkezleri cisim iple tavana asılarak bulunur. Şekil 1 deki cisim tavana asıldığında ağırlık merkezi ipin doğrultusu üzerinde bir yerde olur. Böyle olmalıdır çünkü ancak o zaman net moment sıfır olabilir. Aynı cismi şekil 2 deki gibi farklı bir noktadan asarsak ağırlık merkezi yine ipin doğrultusu üzerinde olacaktır. İşaretlenen doğrultuların kesiştiği yer ise cismin ağırlık merkezidir.
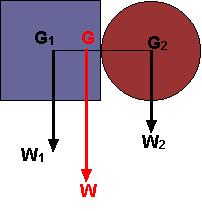
Yukarıdaki şekilde kare ve dairenin ağırlık merkezleri G1, G2 ; ağırlıkları ise W1, W2 ile gösterilmiştir. İki levhanın birleşmesiyle oluşan cismin ağırlık merkezi levhaların ağırlıklarının bileşkesi alınarak bulunur. (paralel kuvvetlerin bileşkesi) Yeni cismin ağırlık merkezi G, ağırlığı ise W ile gösterilmiştir.
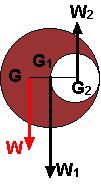
Yukarıdaki şekilde G1 merkezli daireden G2 merkezli küçük daire kesiliyor. Oluşan yeni cismin ağırlık merkezi G noktasıdır. G noktasının yerini bulabilmek için W1 ve W2 nin zıt yönlü paralel kuvvetlerin bileşkesine göre bileşkesi bulunmalıdır.
|
|
 |
|
|
|
|
|
En Rahat =} ÖzCaN
En Kırık =} MuRaT
En Asabi =} MeRvE
En İmam =} NeVrİyE
En Çapkın =} SaMeT
En Baba =} HaKaN
En Alem =} BuRaK aLeM
En Sorun =} BüŞrA
En Satranç =} SeMiYe
En Ekol =} OzAn
En Uykucu =} EkReM
En Testo manyaq =} Seda
En Mantık =} ZeHrA
En Bayık =}GöKaY
En Masum =}Alİ
En SakSuAt =} Saİt
En Ajan =} GaMzE
En Erken =} TaNeR
En Death =} EzGi
En Dağınık=} SaLiHa
En Derskolik =} SeÇiL
En Kendi =} ÖzNuR
En Kanka =} aNıL
|
|
|
|
|
|
|
________________________________
|
|
|
 |
|
| |
|
|
